Hello Everyone 🙂
Today I am going to show you my python implementation of the “mating algorithm” as seen in the MIT open courseware 6042j Mathematics for Computer 

You can view and download the algorithm from here: https://github.com/PierpaoloLucarelli/6.042-Mathematics-for-computer-science/tree/master/mating-problem

What is a graph matching problem? 

Graph matching algorithms have the goal of creating matches between nodes in a graph, while minimising or maximising a cost. the cost is usually an identifier of how good a certain match is. This is a problem that comes up a lot in online dating where, as we can imagine there is a need to match couples (nodes) that are compatible (have high cost). For example let’s consider the following graph:

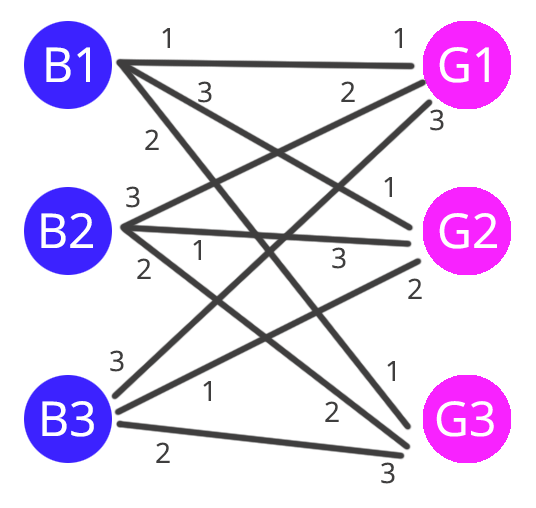
In the graph above, there are 3 boys and 3 girls all connected to each other. The connections indicate a possible match between a boy an a girl and the number associated with the connection is the preference of that boy / girl in numerical ode. For example if we consider boy1, we can see that his preference in order are {G1, G3, G2} where G1 is the preferred girl and G3 is the least preferred. Note, that preferences are not symmetrical. i.e. if G1 is the preference of B1 it doesn’t mean that B1 is the preference of G1.

The mating algorithm

The goal of the mating algorithm is to match each boy with a girl, while minimising the discontent in the matches and the number of rogue couples.

A Rogue couple is a boy and a girl that prefer each other more than the person that they were assigned to. For example if we create the following match in the graph above:

• (B1,G2)
• (B2,G3)
• (B3,G1)

The rogue couple would be (B1,G1) because they prefer each other more than their current partner.

A stable marriage, instead would be one where there are no rogue couples, for example:

• (G1,G1)
• (B2,G3)
• (B3,G2)

If you check, there should be no rogue couple in this matching.

How does the algorithm work?

The algorithm works as follows (Taken from the MIT ocw site)

Repeat for Each Day:

• Morning:
  • Each girl stands on her balcony
  • Each boy stands under the balcony of his favorite girl whom he has not yet crossed off his list and serenades.
  • If there are no girls left on his list, he stays home and does 6.042 homework.
• Afternoon:
  • Girls who have at least one suitor say to their favorite from among the suitors that day: “Maybe, come back tomorrow.”
  • To the others, they say “No, I will never marry you!” (ouch)
• Evening:
  • Any boy who hears “No” crosses that girl off his list.

Here is my Python implementation of the dating algorithm for solving the stable marriage problem.

import numpy as np
N = 5

boys = []
girls = []

def random_preferences():
	return np.random.permutation(N).tolist()



def mating_algorithm(n, boys, girls):
	balconies = [[] for i in range(N)]
	# morning
	while(terminating_condition(balconies) == False):
		for i in range(n): # each boy
			if len(boys[i]) != 0:
				pref = boys[i][0]
				if(i not in balconies[pref]):
					balconies[pref].append(i)
		# afternoon
		for i in range(n):
			if(len(balconies[i]) >= 2):
				choice, rejects = get_girl_preference(balconies[i], i)
				balconies[i] = [choice]
				# evening (remove girl from list of preferences)
				for i in range(len(rejects)):
					boys[rejects[i]].pop(0)
	return balconies

def get_girl_preference(balc, girl):
	g_pref = girls[girl]
	for i in range(N):
		for j in range(len(balc)):
			if(g_pref[i] == balc[j]):
				choice = balc[j]
				balc.pop(j)
				return choice, balc

def terminating_condition(balconies):
	for i in range(len(balconies)):
		if(len(balconies[i]) != 1):
			return False
	return True

for i in range(N):
	boys.append(random_preferences())
	girls.append(random_preferences())

matches = mating_algorithm(N, boys, girls)
print(matches)